The work in this dissertation is related to the development of novel techniques for the processing of signals defined on the sphere. Known as spherical signals, these are encountered in areas of science and engineering where the underlying geometry of the problem has a spherical configuration, e.g., in astronomy, cosmology, acoustics, medical imaging, geophysics and wireless communication. In most of these areas, acquired signals are almost always marred with unwanted, yet unavoidable noise due to different sources of interference, which places signal filtering and estimation at the heart of signal processing methods. In this context, the first part of the dissertation addresses the problem of signal estimation on the sphere in the presence of random anisotropic noise.
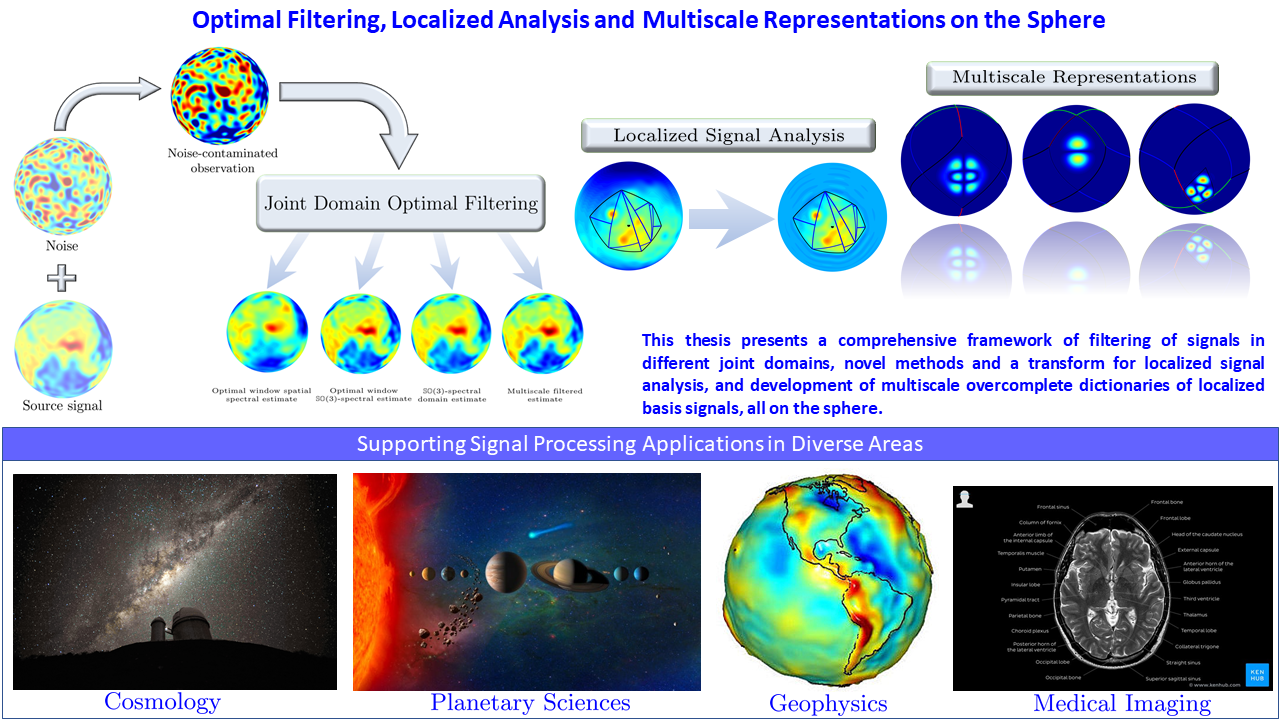
Signal analysis on the sphere can be classified as global and local. In global analysis, signals are considered over the whole sphere and are most commonly represented in terms of spherical harmonic functions. However, the data may not be available, or may not be reliable, over some regions on the sphere, which invokes the need for localized signal representations. One such localized basis for accurate representation of signals over spherical regions, called the Slepian basis, is obtained through the solution of Slepian spatial-spectral concentration problem on the sphere. The second part of this dissertation is focused on the use of Slepian basis functions to support localized signal analysis on the sphere. Analytical formulation for the (i) surface integration of signals, and (ii) computation of Slepian basis functions, over simple spherical polygons is presented. Furthermore, a subset of Slepian basis is employed to formulate a new joint spatial-Slepian domain representation of spherical signals through the novel spatial-Slepian transform. A framework for generalized linear transformations in the joint spatial-Slepian domain is also presented, which is exemplified through optimal filtering on the sphere.
The third part of this dissertation considers the use of Slepian basis functions for multiscale (multiresolution) analysis of spherical signals through hierarchical partitioning of the sphere into pixels of varying spatial extent. In this context, different sampling/partitioning methods on the sphere are reviewed and a Hierarchical Equal Area iso-Latitude iso-Longitude Pixelization (HEALLPix) scheme is proposed. Employing the formulation available in the literature, an overcomplete multiscale dictionary of Slepian functions is constructed. Additionally, a framework for analytical computation of Slepian functions for pixels generated using Hierarchical Equal Area iso-Latitude Pixelization (HEALPix) scheme is formulated, which facilitates the construction of another multiscale overcomplete dictionary of Slepian functions on the sphere. Both dictionaries are analyzed for the span and mutual coherence of their elements.