LUMS is a Shangri La for interdisciplinary work. It offers the right mixture needed to create memorable experiences through the cross-pollination of different schools, courses, and faculty; a win-win situation for passionate learners. Two students of Dr. Zahra Lakdawala, who is a faculty at the Department of Mathematics at SBASSE, from the Quantitative Finance, FINN422, (sometimes referred to as QuantFinn in this story) course have been accepted to MIT, Oxford, and McGill. They are Ahmed Salman and Muhammad Ibrahim who hail from the Suleman Dawood School of Business (SDSB) and took this course from Dr. Zahra during the Spring 2021 semester.

“Both of them are SDSB students. Muhammad Ibrahim is also graduating as a CS minor. MIT is intense with its admission process and its round of interviews. This is where Ibrahim said the course and its content, particularly the modeling and applying it using python packages for solving really helped!”, said Dr. Zahra, recalling the work of one of her students involved in this story.

Ahmed Salman, while commenting on the course said "The course I took with Dr. Zahra was one of the most rigorous experiences of my degree. Besides managing an A+ grade, I saw myself intellectually challenged at every step of the way. With the intensive assignments and especially the final project, I used the reference of over 5 textbooks to get through them. Besides coursework, it also piqued my general interest in the subject, as I read books on Chaos Theory and Jim Simons, both topics that I discussed in her office hours.” Wrapping up his thoughts, he said “I can confidently say that this course gave me a solid grounding in quant-finance concepts and will surely complement my higher studies."

Muhammad Ibrahim, who got admission offers from MIT, Oxford and McGill said, "Applying to MIT and getting an admission wouldn't have been possible without taking QuantFinn from Dr. Zahra, and without her recommendation for admissions. I am extremely grateful for the help! "

Let’s take a closer look at the final year project of Ahmed Salman and Muhammad Ibrahim, which garnered the attention of Dr. Zahra and her colleagues, particularly the detail of work displayed by the two brilliant students.

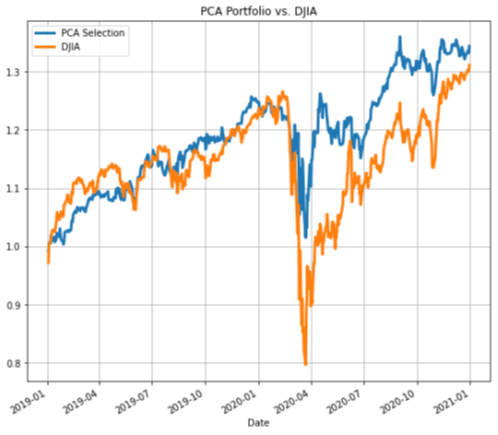
First, the students had to construct a portfolio that maximizes shareholder returns. “We started with the stocks in the DJIA index as a well-diversified portfolio. We evaluated four approaches of weighing these stocks in our ideal portfolio.” The first one prioritized stock with the highest eigenvalues based on their principal component analysis. Because the largest vectors explain most of the stock variation, the hypothesis here was that this portfolio would match the market index while reducing risk.

Sure enough, the portfolio seemed to beat the market index while also exhibiting lower volatility.

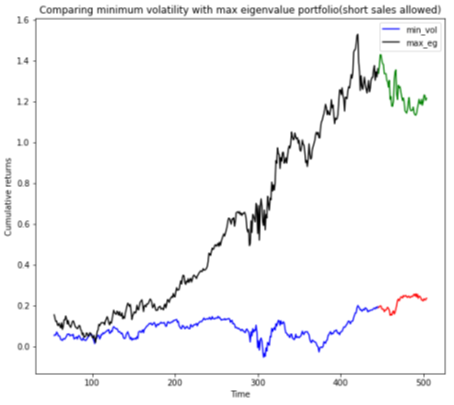
They also compared this with weights assigned to stocks based on allowing short sales to minimize variance.

The two portfolios were also judged in performance by looking at their performance over the historical time series period, by dividing it into an in sample and an out sample (which consisted of the last 60 days). Clearly, the portfolio with the maximum eigenvalue (a special set of scalars associated with a linear system of equations) performed better but was also more volatile.

The students then compared these approaches with another portfolio based on maximizing Sharpe ratio weights in the chart below:

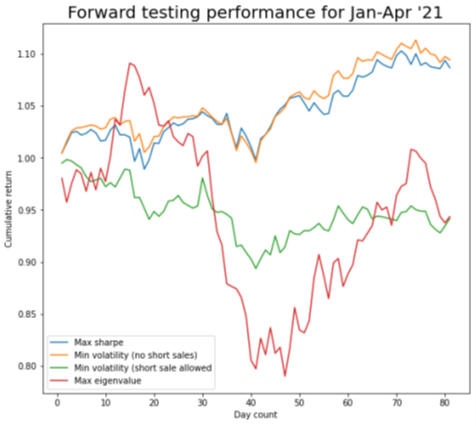
The second portfolio generated the highest returns at 9.4% while the portfolio with the maximum Sharpe ratio we computed from the efficient frontier, giving a return of 8.6%. However, the team conclude that the best strategy was to follow the weights of the maximum Sharpe ratio portfolio, as they will beat the market over the long run and give a good risk-adjusted return.

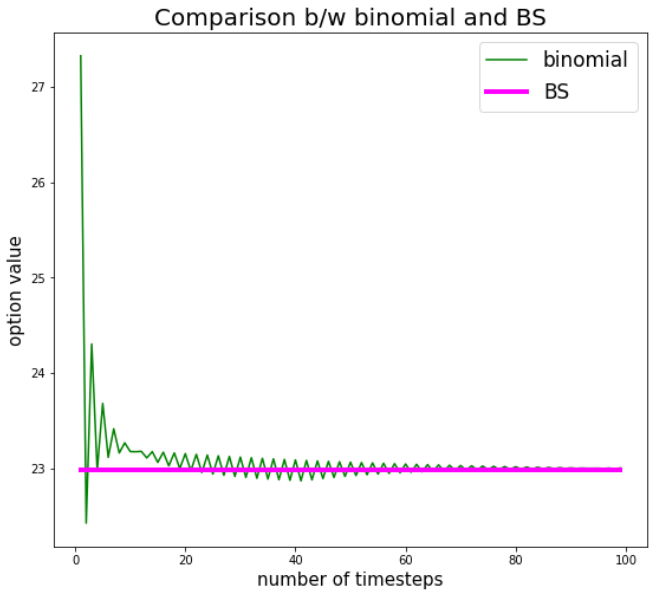
Regarding Option Pricing, the team said “In the second question, we approximated the value of a call option on Apple (AAPL) with the numerical solutions to the Black Scholes model. We used three approximation methods: binomial, Monte Carlo and finite differences. Our biggest takeaway here was the importance of being granular enough in using these approximations, such that they divide the target time period into smaller frames or ‘timesteps’ as call them – for them to accurately price options. For the binomial approximation, we found that it accurately matched the Black-Scholes model but only for smaller timesteps.”

Next, the Monte Carlo method modelled underlying prices using geometric Brownian motion. Although for smaller simulations, there are significant differences between the different models, they found that for larger simulations, all schemes converge to the Black-Scholes pricing.

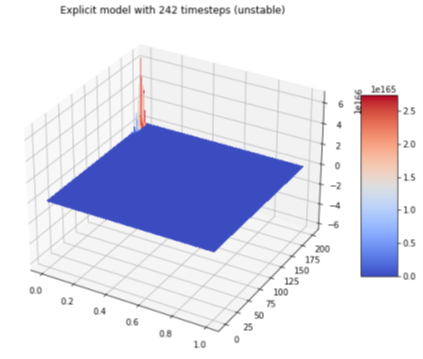
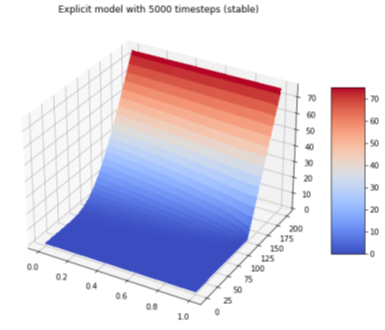
Referring to the most challenging bit, “the finite difference scheme was the most challenging for us.” Here, they compared two schemes: explicit and implicit. While the explicit scheme calculates the state of a given system at a different time from the current time, the implicit scheme a solution by solving an equation that includes both the current and later states of the given system. They found that here too the explicit scheme came with a Neumann condition, which required more granular timesteps for it to generate a useful output, as shown below:

Reflections by Ahmed Salman

Before this course, I had taken courses in finance, CS and some in mathematics, but didn’t feel like these subjects could be integrated. But FINN422 was an incredible experience because it combined the three subjects together into a holistic experience for us. It forced us to reconcile the financial concepts, mathematical equations, and programming tools we already knew to build a coherent picture in our minds. I still remember being very overwhelmed by the initial assignments in this course, fumbling with endless equations and coding challenges, but looking back, I’d do it all again. While it was a very rigorous course, I came out of it with much more than a good grade. It gave me the confidence to adapt to unfamiliar subjects and really get comfortable in my own skin as I navigate them!