Abstract

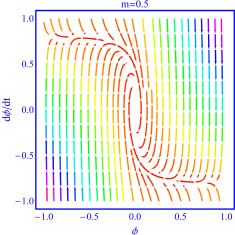
In this thesis, we examined the semi-classical dynamics of a polymer quantized scalar field in cosmology subject to a combination of a quadratic and a cubic potential in cosmology.  

Polymer quantization is a quantizing procedure that is motivated by LQG (Loop Quantum Gravity). The prescription here is different from the Schrodinger quantization scheme, as one of the quantum operators (either position or momentum) in it is not well-defined. At a particular scale, the polymer quantization and Schrodinger quantization methods become equivalent.

In our problem, we chose the scalar field operator to be undefined. We used the semi-classical approach by polymer quantizing our Hamiltonian by calculating the expected values of the cubic and the quadratic scalar field. We then observed the dynamics of the semi-classical scalar field in the background FLRW (Friedmann-Lemaitre-Robertson-Walker) spacetime. We also compared our results with the known quadratic field potential case. We also contrasted our results with the research outcomes in which the momentum operator was not well defined. We found the early inflation period to be absent and the scalar field to be oscillating at higher magnitudes.

Zoom link: https://lums-edu-pk.zoom.us/j/94032652158?pwd=OW1PbFpOSHR1Nlp3amRFcGxnQjU5dz09